Last time we looked at well-centered polytopes and I wondered whether a vertex-transitive polytope with well-centered \(j\)-faces would be completely well-centered. (For \(j=0\) or 1 the condition is trivial, since points and edges are always well-centered, so we’d have to require \(j=2\) at least.) This seems to be false. But why would I think this?

A completely well-centered polytope is what I’ve called orthodivisible: it can be split into orthoschemes—simplices whose vertices are on a path \(P_0, \dotsc, P_d\) with mutually orthogonal edges.

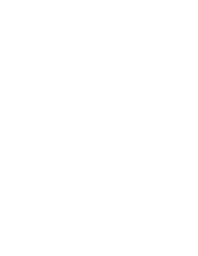
That’s because you can make a path starting at a vertex—let’s call it \(P_0\)—continuing to the midpoint of an edge—\(P_1\)—and through the circumcenters of \(j\)-faces, up to the center of the whole polytope, and all the edges are mutually orthogonal.

They’re mutually orthogonal since the circumsphere \(S_F\) of each face \(F\) is the intersection of the affine span of \(F\) with the circumsphere of the whole polytope \(P\), and the normal vector from the circumcenter \(c\) of \(P\) through any subspace \(\operatorname{aff}(F)\) meets it in the center of \(S_F\).

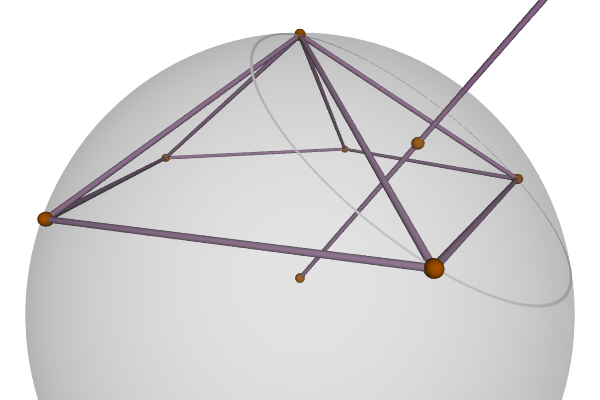
Some circumscribable polyhedra with regular 2-faces aren’t well-centered, like the pentagonal pyramid J2:

or a square rotunda:

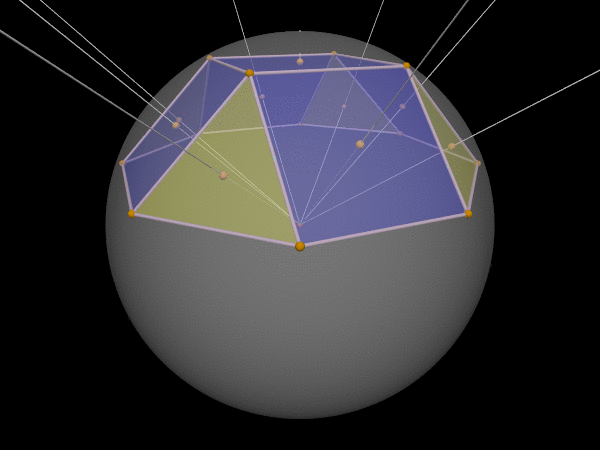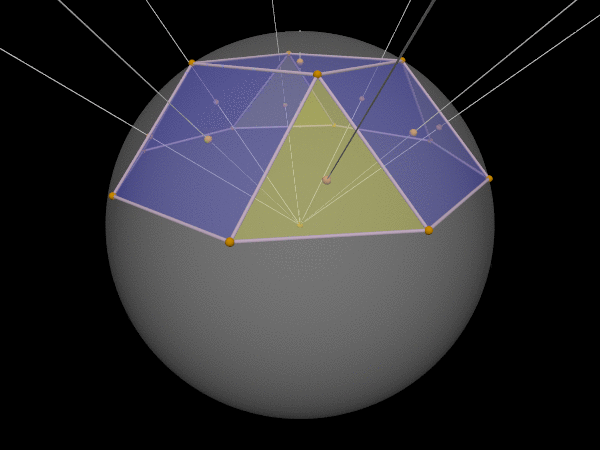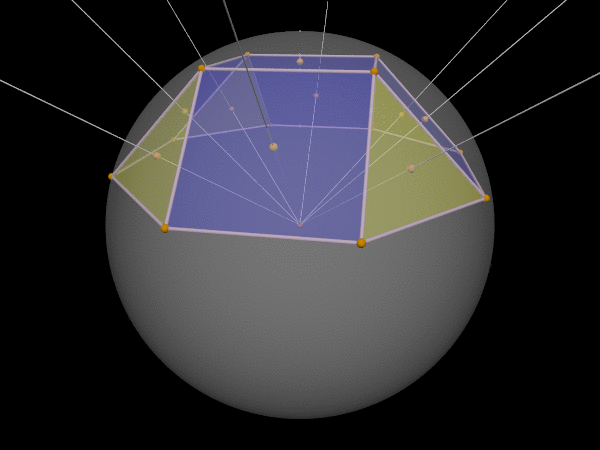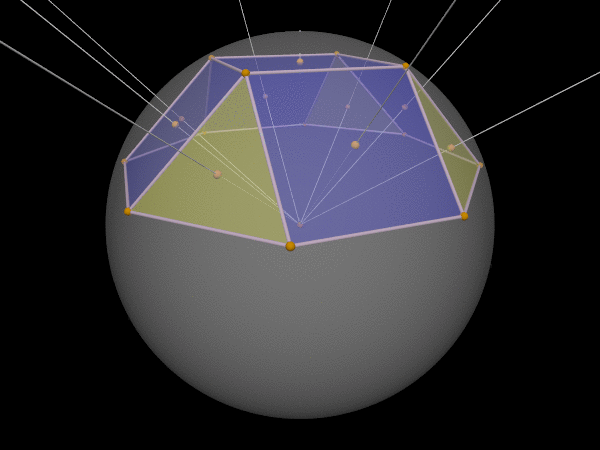
Although the normal lines through each face’s circumcenter all meet in one point—the polytope’s circumcenter—that’s outside the polytope.

These problems occur because the polytope’s faces don’t “surround” the whole sphere: and so the meeting point of the normal lines through the faces’ circumcenters might not be inside.

A vertex-transitive polytope, though—or indeed a polytope whose symmetries act transitively on all the faces of any particular rank—must surround the sphere in the right way. Even in a vertex-transitive polytope, though, the 2-faces might not be well-centered. Consider the disphenoid frustum from last time, with its affine spans and normal lines:

In combination, though—well-centered 2-faces in a vertex-transitive polytope—it seems like looking within a 3-face at the point where the normal lines through each of its 2-faces’ circumcenters meet, which is the 3-face’s circumcenter, might have to be in the interior.

Yet spidrox puts the kibosh on that.

It’s vertex-transitive, with regular 2-faces, but its square pyramid facets are not well-centered. Notably, they’re barely not well-centered: the circumcenter lies in the boundary.

Could strengthening a bit more—to vertex- and edge-transitive poltyopes—mean that the 3-faces must be well-centered?